Smoothing

Words Of Wisdom about Smoothing:

Smoothing prescriptions should answer the question: what would the data look like if the observer could average many, many scans?

If one could make many measurements of a sample, and stack scans, the underlying features of the physical process would be revealed, without any sacrifice in resolution. The final averaged smooth curve, called the parent spectrum, is the desired result.

The purpose of a good smoothing formula should be to provide an estimate of the parent spectrum from which a particular noisy sample (spectrum, mass spectrum, chromatogram) was drawn. This estimate should be formulated from physical knowledge about the experiment that can be agreed upon in advance. The formula should not contain any arbitrarily chosen parameters.

If you are currently using a smoothing function, here is a way to test it. Smooth your data. Then smooth it again. If the second smoothing changes the result of the first smoothing, then you should think about using a better function.

Smoothing algorithms have one of two goals: to make the data look better; or, to reveal data partially obscured by noise. We view the former as a corruption of the data; it cannot be justified from the formal principles of Maximum Likelihood (ML) data analysis. We do not offer this option. On the other hand, the separation of signal from noise is a legitimate goal of an ML process. How might one carry it out?

First, one must bring information to the operation which is not explicit in the data, and which differentiates signals from noise. One immediately thinks first of peakshapes, the signature of the signal, and then of statistics, the characteristic amplitude distribution in the data in the absence of a signal. These two discriminants, encoded into a suitable algorithm, can select signal-like features from data, discarding noise-like features along the way. So we ask the user to specify: (1) Does the noise follows Poisson (counting, or signal-dependent) or Gaussian (additive, signal-independent) statistics? (2) What does the narrowest data peak look like? We then solve the following problem: Given these two constraints, what is the most likely spectrum one would see if there were no noise?
Experimentally, that answer may be obtained by averaging very many identically prepared data sets together - a process not usually practicable, either because of the time required, or because the data source is not that stable. However, Maximum Likelihood and Maximum Entropy methods may be utilized to calculate the most probable spectra that such averaging would produce if one could carry it out. The additional constraints described above make such a calculation possible. (The theory and equations are fully described in "Maximum Likelihood smoothing of noisy data", published in American Laboratory, March 1990, as well as in all Razor manuals).

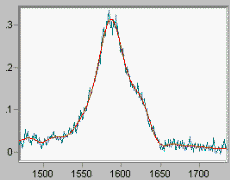
	Fig 1 shows a noisy Raman spectrum (the noise is additive Gaussian) overlaid by the algorithm's estimate of the signal in the absence of noise. Note that the signal peaks are not distorted by the operation. We have not smeared the signal to reduce the visibility of the noise; we have instead constructed from the given data the spectrum most likely to represent the signal in the absence of noise.
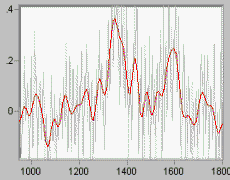
Fig 2 shows a VERY noisy chromatography sample overlaid by the "smoothed" result. This is signal estimation in the presence of noise.

Return to homepage