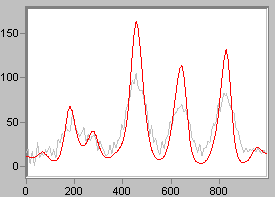
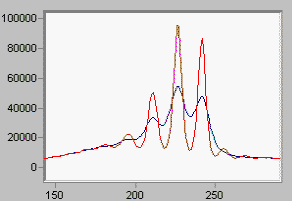
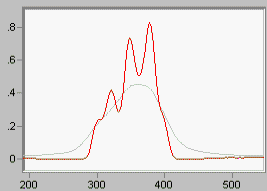
Deconvolution

Deconvolution, removing instrumental broadening, need not be an untamed operation with many different answers. Clearly the desired result is not the largest spectrum, nor the smallest, nor the prettiest, but the most likely spectrum that a better instrument with a narrower bandpass would produce. So we construct a function which maximizes that probability. We ask for the most likely output that a hypothetical "better instrument" would produce. The resulting algorithm depends upon the noise statistics, which may be either Gaussian, signal-independent (additive), or Poisson, signal-dependent (counting event). It also contains other explicit constraints (for example, positivity) which the nature of the data requires. The most common of these is the informational entropy of the output spectrum, which should be maximized if the result is to be a maximum entropy spectrum. The constraint of the broadening function of the instrument that took the data is obviously also needed. The better this is known the better the results.
We offer four deconvolution functions, DEC, LUC, ASH and LME. Two of them, DEC and LME, are Maximum Entropy deconvolution functions specifically tailored for data with gaussian noise statistics, such as infra-red. Two are Maximum Likelihood deconvolution methods for data with Poisson (counting) noise statistics, such as encountered in xray spectroscopy. One of the Maximum Entropy functions accepts a Bayesian prior.

Fig 1 shows a DEC (Maximum Entropy) deconvolution of a UV spectrum (benzene) overlaying the data. The operator used a measured peakshape of an experimental peak known to be much narrower than the instrument function. This is the best way to obtain an instrument function. Measure it. This is a remarkable result; rarely will you do better! The instrument function was very well known and the noise was low.

Fig 2 shows the same DEC algorithm applied to noisy data. This is as far as it went because this is as far as it should go.

Fig 3 shows a LUC deconvolution of a Poisson spectrum of x-ray data. LUC is a Maximum Likelihood algorithm due to Lucy. This time we used a peakshape derived from the data itself. (Sometimes that's all one has.) A factor of two to three is about the best LUC will do; but the Lucy algorithm is very robust and it is rare to come up empty handed because of instabilities even if the spread function is not quite right. It's a good choice even for Gaussian statistics if the instrument function is not well known.

One can get higher resolution than LUC will produce in an acceptable number of iterations, by using a pre-processor starting function. ASH works this way; the starting function is produced by a linearized version of the Maximum Entropy algorithm. Fig 4 shows the result of such a marriage. The spectrum is again a Raman spectrum, this time of sulfur. A characteristic multiplet, not resolved even at 1 /cm, is shown here taken at 2/cm, with the result of ASH superimposed. You certainly can't count the peaks by eye in the original data!

Linear deconvolution is sometimes useful because it is fast, and does not enforce positivity. Not every spectroscopy is positive! (Think of first derivative NMR data). LME is the linear form of the Maximum Entropy function DEC. If you want a linear algorithm that is not iterative, and permits negativity (all linear algorithms do), this is the way you should go. Noise is properly accounted for.

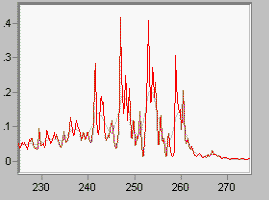
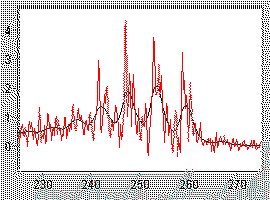
Fig 5 shows the same data as Fig 1, with the output of LME overlaid.

Many other deconvolution algorithms are known. One class allows you to fiddle with the constraining parameters until you get something you like. Fourier Self-Deconvolution is an example. Avoid these, all of them. Most of them take no account of noise. They permit you to get about any spectrum you want out of your data, so you have to know the answer before you ask the question, or you may get garbage. But if you know what the spectrum should look like, why even take data? The purpose of data processing of any kind is to improve your state of knowledge.

Back to homepage