Bayesian Derivatives

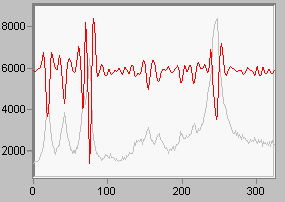
Spectroscopists frequently use derivatives of the spectrum to extract information. Differentiation is not really a stable mathematical process, so the rule is that differentiating a noisy signal will amplify the noise.
Smoothing a derivative is not quite the right thing to do. The right thing is to compute the most probable derivative from the infinite ensemble of noisy derivatives that noisy samples from the same process could produce. That is what we do, using a process known as Bayesian analysis.

Shown in Fig 1 is the second derivative of a rather noisy signal. Note the complete absence of noise in the result. We are not removing the noise, but estimating what the derivative would look like if there were no noise.

Not everyone needs a Bayesian differentiator, but if you do, you really need ours. It will handle derivatives of all orders.

Back to homepage